Microsoft Solver Foundation is an exciting new .NET based optimization platform that includes solvers for Linear Programming (LP), Mixed Integer Programming (MIP), Quadratic Programming (QP) and CSP (Constraint Programming) problems. Included in version 1.1 is the high-performance state-of-the-art multi-threaded Gurobi MIP solver and plugin capabilities for third party solvers such as Cplex and Mosek. We can provide services to help you design, prototype, develop and implement high-performance, scalable and reliable optimization models on this framework. Models developed in Microsoft Solver Foundation can be integrated seamlessly in your .NET applications and services.
Below is a list of toy models that are discussed in the above document. The size of the models is kept small so they can be solved with the Standard Edition of Microsoft Solver Foundation. These small toy examples are used to demonstrate certain features of OML. Real world applications are often too large, too specific and too messy to be very useful for demonstrations, while these smaller examples show features that can be used directly in larger contexts.
Model number one of the GAMS model ibrary is this
transportation model from the famous book by George Dantzig (Linear
Programming and Extensions, Princeton University Press, 1963). It has been
slightly changed to introduce dual degeneracy, so several optimal solutions
exist. Although this linear programming problem is very small it demonstrates
indexing and scalable formulations. We argue that OML is a step forward from
using Excel Solver as it shows rather than hides the structure of the model.
GAMS and
Excel work with sparse data: missing data or empty cells are considered to be
zero when using operations such as summations. The Data Binding facility in the
MSF Excel plug-in requires a "dense" data representation. Here we show two
possible solutions: first in the diet model we augment the data with the zero
values. In the maximum flow network model we show how we can enumerate the set
of arcs so we don't need to specify non-existing arcs.
Constructing Magic Squares is difficult to model efficiently
using Mixed Integer Programming. A magic square has numbers 1,..,n2
placed on the board such that the rows, the columns and the diagonals add up to
the same value. The problem can be expressed much more natural with a CSP
solver using the all-different constraint. Some non-standard solver
options were required to achieve better performance.
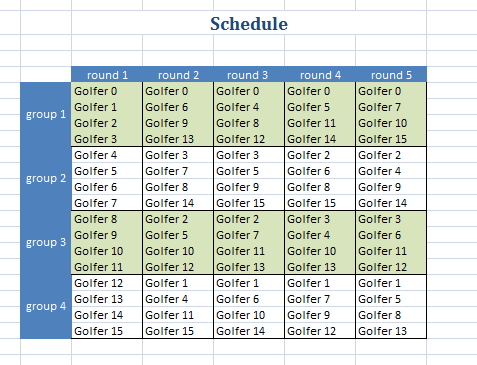Constructing a schedule for a golf trip where players don't play each other
more than once is a difficult problem. Here are some formulations for N=16
golfers playing 5 rounds with 4 foursomes. These models solve fairly easily.
The same problem with N=32 golfers, 10 rounds is very difficult and I was not
able to solve that instance.The models are implemented as CSP models: they are more compact than the corresponding MIP models. Scheduling models are a well-know application area for CSP algorithms.
The
traveling salesman problem (TSP) is a famous difficult problem. A salesman has
to visit a number of cities and return to the starting point. The goal is to
minimize the total distance traveled. The TSP problem is probably the most
studied problem in the OR field. Here we solve a small instance as a MIP.The current state-of-the-art MIP solvers can solve TSPs up to about 50 cities, and find good solutions for even larger problems. Of course specialized algorithms and solvers are capable of handling larger instances.
Computing Langford sequences can be specified easily using
the all-different constraint. The problem is to place the numbers
(1,1,2,2,3,3,4,4) such that equal numbers k have k other numbers in between,
e.g. (4,1,3,1,2,4,3,2).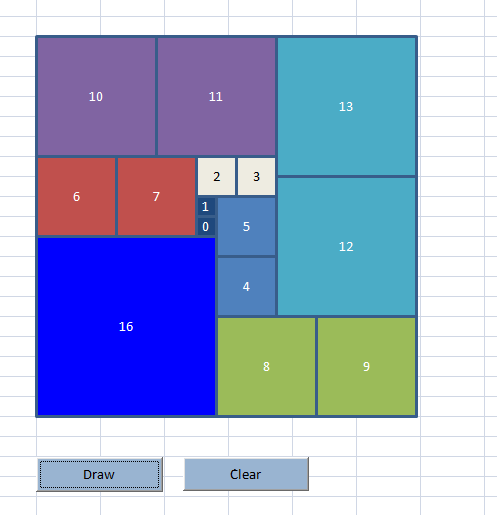
Tiling squares with an upper limit on how many duplicate tiles can be used. The (7x7)
problem below is easy we assume we know that we can cover the (7x7) are with
tiles (4x4), (3x3), (3x3), (2x2), (2x2), (2x2), (1x1), (1x1), (1x1). The (9x9)
problem is more difficult: we have an inventory of three tiles of each size
(1x1) through (8x8) but not every tile has to be used. The big (19x19) problem
is solved with a pool of just two tiles of each size (1x1) through (16x16).
Modeling tricks to reduce symmetry are applied to be able to solve the larger
instances.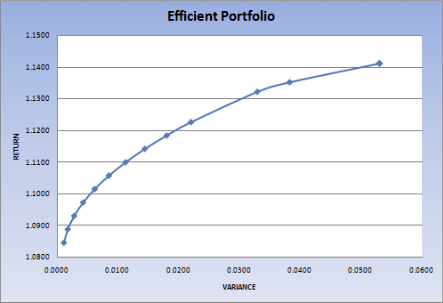
Quadratic Programming (QP) models can be used to model a
portfolio optimization problem. When we want to draw an efficient frontier a
simple algorithm is to solve several QP's. Unfortunately there are no looping
constructs in OML: we can form and solve only a single model with the Excel
plug-in. In this example we combine the QP's into a single large QP.
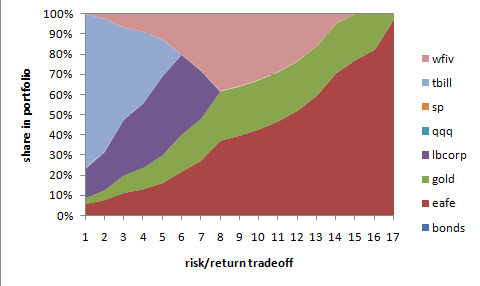
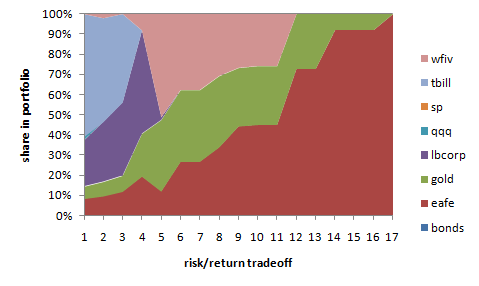In this model we compare an LP
formulation with a QP formulation for the portfolio model. The multiple models
are handled by a piece of C# code which is compiled into a DLL. Inside the C# code
we express the models in OML. The DLL is called from Excel via some VBA code.
The output reports in the form of graphs are created in Excel.
A remarkable algorithm to solve Cutting Stock problems is based on Column Generation, where new
variables (columns) are added to an LP model. In the document above a simple implementation
of a column generation approach is implemented using MSF. The method is applied to a standard
cutting stock problem where rolls of raw material have to be cut while minimizing waste.
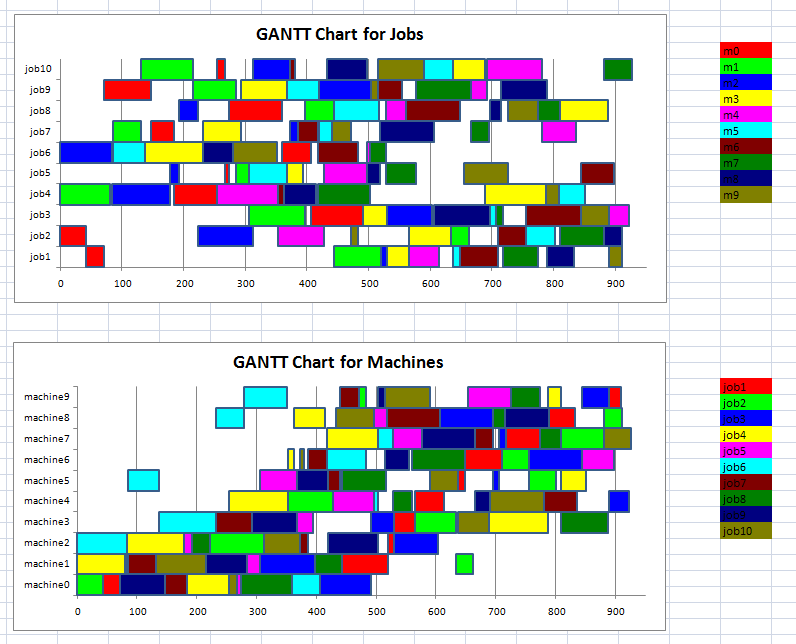Job Shop Scheduling problems can be difficult to solve. An example is ft10 with 10 jobs and 10 machines.
An optimal solution for this problem was not known for 25 years. Nowadays with the best MIP solvers
such as Gurobi and Cplex we can solve this problem formulated as a standard MIP model in less than 5 minutes.
Some VBA code has been developed to produce GANTT charts in Excel.